Data Graph Solving
Was asked an interview whiteboarding question that was using a data graph and to solve two problems. I don't like whiteboarding sessions as I don't think they have a good application to what software in practice is and how to solve them. They sit as isolated puzzles that can be expressed by programming with clear inputs and outputs, but that is never the case with any system I have created or worked on so alas in my opinion worthless except for showing can candidate solve an academic problem they saw in a textbook and class.
The best interview is to do real work on production code, the second best interview is to take a complete project that the applicant has made and make some improvements in it during the time you are working i.e. (add tests, a new plugin module, dependency injection etc), as they should know the limitations and how to modify it as needed much like what would happen at your job.
Back to the graph data problem as I want to demonstrate several ways to solve the issue and each in a different manner that shows no solution is the best and there are tradeoffs to each.
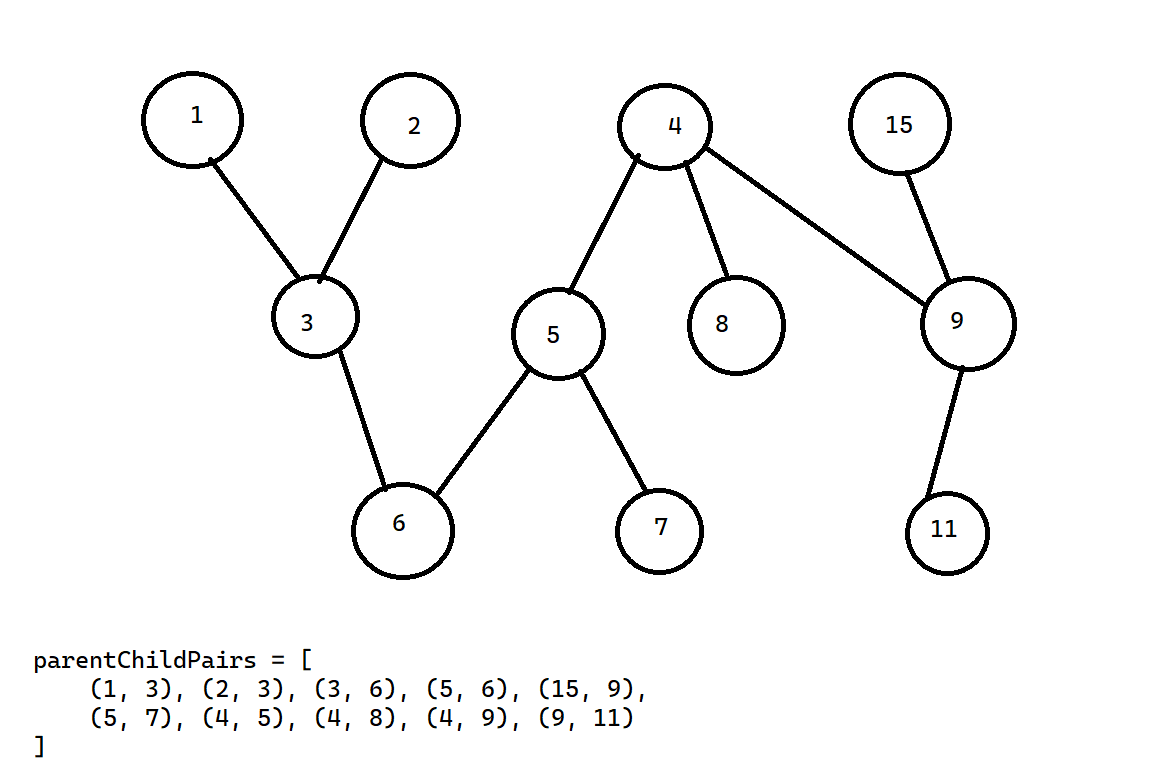
Here is a visual representation of the problem. Here the nodes are defined as bi-directional connections between nodes with a tuple to define the relationship
Problem Input:
Construct a data structure that will allow you to represent and solve for this input
parentChildPairs = [
(1, 3), (2, 3), (3, 6), (5, 6), (15, 9),
(5, 7), (4, 5), (4, 8), (4, 9), (9, 11)
]Find:
Write a function that takes this data as input and returns two collections: one containing all individuals with zero known parents, and one containing all individuals with exactly one known parent.
Expected Output:
[1, 2, 4, 15], // Individuals with zero parents
[5, 7, 8, 11] // Individuals with exactly one parentC# Rough Solution
I created this solution during the timebox and it works alright, but definitely could be improved. The first answer is do a set difference as all parents minus children where ids match will give you all the parents with no known parents or graph roots.
The second part I stumbled around a little, but then got it after thinking all I need to do is reverse the graph and count the parents of every child if a child only has one parent then it is added to the set of ids that indicate a single parent
using System;
using System.Collections.Generic;
using System.Linq;
public class Results
{
public List<int> Answer1 { get; set; }
public List<int> Answer2 { get; set; }
}
class Solution {
/// The time is linearly bound as each new element will increase the loop and at this time there are N !--ies/
/// passed over 2 times at least so 2 X N
static Results findNodesWithZeroAndOneParents(List<int[]> inputPairs)
{
var leftSide = new List<int>();
var rightSide = new List<int>();
var answer1 = new List<int>();
var answer2 = new List<int>();
var flattenedGraph = new Dictionary<int, List<int>>();
foreach (var inputPair in inputPairs)
{
var startNode = inputPair.First();
var endNode = inputPair.Last();
leftSide.Add(startNode);
rightSide.Add(endNode);
if (!flattenedGraph.ContainsKey(endNode))
{
var newList = new List<int>();
newList.Add(startNode);
flattenedGraph.Add(endNode, newList);
}
else
{
var currentChildren = flattenedGraph[endNode];
currentChildren.Add(startNode);
flattenedGraph[endNode] = currentChildren;
}
}
answer1 = leftSide.Except(rightSide).ToList();
foreach (var node in flattenedGraph.Keys)
{
var parents = flattenedGraph[node];
if (parents.Count() == 1){
answer2.Add(node);
}
}
return new Results {
Answer1 = answer1,
Answer2 = answer2
};
}
static void Main(String[] args) {
var parentChildPairs = new List<int[]>() {
new int[]{1, 3},
new int[]{2, 3},
new int[]{3, 6},
new int[]{5, 6},
new int[]{15, 9},
new int[]{5, 7},
new int[]{4, 5},
new int[]{4, 8},
new int[]{4, 9},
new int[]{9, 11}
};
var results = findNodesWithZeroAndOneParents(parentChildPairs);
Console.WriteLine($"Answer 1: {string.Join(",",results.Answer1)}");
Console.WriteLine($"Answer 2: {string.Join(",",results.Answer2)}");
}
}C# Results
Answer 1: 1,2,15,4
Answer 2: 7,5,8,11After doing this I got to thinking there are other languages to do this and since the operations are set oriented then use a set language like SQL will yield a valid solution so I came up with this. I am using MS SQL 2017 as it supports graphs and am experimenting with it now and came up with this
MS SQL 2017 Solution
DROP TABLE IF EXISTS Connections
DROP TABLE IF EXISTS Parents
CREATE TABLE Parents (
Id INT NOT NULL
) as NODE;
INSERT INTO Parents
Values (1),
(2),
(3),
(5),
(15),
(4),
(9);
GO
DROP TABLE IF EXISTS Children
CREATE TABLE Children (
Id INT NOT NULL
) as NODE;
INSERT INTO Children
Values (3),
(6),
(9),
(7),
(5),
(8),
(11);
GO
DROP TABLE IF EXISTS Connections
CREATE TABLE Connections (
Distance INT DEFAULT 1,
CONSTRAINT Parent_Child CONNECTION (Parents TO Children) ON DELETE CASCADE
) as EDGE;
INSERT INTO Connections
VALUES
((SELECT $node_id FROM Parents WHERE ID = 1), (SELECT $node_id FROM Children WHERE id = 3),1),
((SELECT $node_id FROM Parents WHERE ID = 2), (SELECT $node_id FROM Children WHERE id = 3),1),
((SELECT $node_id FROM Parents WHERE ID = 3), (SELECT $node_id FROM Children WHERE id = 6),1),
((SELECT $node_id FROM Parents WHERE ID = 5), (SELECT $node_id FROM Children WHERE id = 6),1),
((SELECT $node_id FROM Parents WHERE ID = 15), (SELECT $node_id FROM Children WHERE id = 9),1),
((SELECT $node_id FROM Parents WHERE ID = 5), (SELECT $node_id FROM Children WHERE id = 7),1),
((SELECT $node_id FROM Parents WHERE ID = 4), (SELECT $node_id FROM Children WHERE id = 5),1),
((SELECT $node_id FROM Parents WHERE ID = 4), (SELECT $node_id FROM Children WHERE id = 8),1),
((SELECT $node_id FROM Parents WHERE ID = 4), (SELECT $node_id FROM Children WHERE id = 9),1),
((SELECT $node_id FROM Parents WHERE ID = 9), (SELECT $node_id FROM Children WHERE id = 11),1)
GO
-- Find end nodes with only 1 parent
SELECT c.Id
FROM
parents p, children c, connections cc
WHERE
MATCH(c<-(cc)-p) -- Trace back from child to parent through connection edges
GROUP BY c.Id
HAVING COUNT(*) = 1
-- Find nodes with no parents
SELECT Id
FROM parents
WHERE Id NOT IN
(
SELECT Id
FROM children
)
ORDER BY Id MS SQL 2017 Results
(7 rows affected)
(7 rows affected)
(10 rows affected)
Id
-----------
5
7
8
11
(4 rows affected)
Id
-----------
1
2
4
15
(4 rows affected)Note you can't make temp tables that are nodes or edges and it creates these relational backed tables into a new area as they have expanded capabilities as graph database tables
Key point on this is to define the MATCH path of nodes to show what you want the graph algorithms to work towards. MATCH(c<-(cc)-p) -- Trace back from child to parent through connection edges Here I am saying go from the Parents table and find all the applicable Children entries along the Connections edges. This is powerful, but this is a small case to show the details, and I can mix in relational dataset row based operations on top of the graph results here with a group by and having count to find paths with only 1 parent
-- Find end nodes with only 1 parent
SELECT c.Id
FROM
parents p, children c, connections cc
WHERE
MATCH(c<-(cc)-p) -- Trace back from child to parent through connection edges
GROUP BY c.Id
HAVING COUNT(*) = 1Python with Networkx
import networkx as nx
if __name__ == '__main__':
parentChildPairs = [
[1, 3],
[2, 3],
[3, 6],
[5, 6],
[15, 9],
[5, 7],
[4, 5],
[4, 8],
[4, 9],
[9, 11]
]
G = nx.DiGraph()
startNodes = []
endNodes = []
for inputPair in parentChildPairs:
startNodes.append(inputPair[0])
endNodes.append(inputPair[-1])
G.add_edge(inputPair[0], inputPair[-1])
no_parents = []
for current_node in startNodes:
parents = list(G.predecessors(current_node))
if len(parents) == 0:
no_parents.append(current_node)
print(set(no_parents))
single_parents = []
for current_node in endNodes:
parents = list(G.predecessors(current_node))
if len(parents) == 1:
single_parents.append(current_node)
print(set(single_parents))Python Results
{1, 2, 4, 15}
{8, 11, 5, 7}I like the idea of the SQL datastore graph best, but find the python code to be the most readable and maintainable.
